|
|
|
|
News The Project Technology RoboSpatium Contribute Subject index Download Responses Games Gadgets Contact Car designConversion of energy during acceleration processIf a force is operating on a car, it is accelerated. While talking about acceleration, we always postulated a constant action of force. When looking at formula number [2.12] we can see that the correlation between kinetic energy and speed is quadratic. If a vehicle is accelerating constantly, i.e. the increase of speed per time interval is constant, the performed work per time interval (=power) is increasing in a quadratic way, too. Stupidly there is always just a limited amount of power available. Expressed in formulas there is:
P = power, m - mass, v - velocity, t - time When using the benchmarks of the project car with combustion engine, there is a maximum power of 17kW available, accelerating a weight of 765kg (with half of the payload). Using formula [2.15b], we get t = 17.4s for the accelerating process from 0 to 100km/h (0 to 27,8m/s). In reality, the car needs more than 30 seconds to speed up to 100km/h. One reason is, that the combustion engine doesn't provide the maximum power at all engine speeds. For the whole accelerating process there is just al lower (average) power available. Calculating the average power for the accelerating process from 0 to 100km/h within 35s, we get a power P = 8.4kW when using formula [2.15a]. The truth lies somewhere in between, because we neglected air resistance and rolling resistance by now. AirresistanceContrary to accelerating processes, the kinetic energy of a vehicle driving with constant speed is constant, too. In practice energy is constantly needed to keep up with the speed. One reason for this is the air resistance. Formular [2.9] shows the correlation between speed and resulting force. At the chapter about work, energy and power we have learned, that energy multiplied by the covered distance equals the needed energy. Expressed in formulas there is:
P - power, ρ - mass density of the air, CW - drag coefficient, A - reference area perpendicular to the direction of movement, v - speed, t - time, s - distance, E - energy Looking at formula [2.16] we can see that the needed power to keep up with constant speed is increasing cubic! So we can see that high speed and cruising range are incompatible. Using the values of the project car (CW=0,47 A=1,51m2) and 1,2041 kg/m3 for the air density, we get:
More than 9kW (13HP) just to overpower the air resistance while driving with a speed of 100km/h, is a lot of power for a electric vehicle with just poor energy reserves available. Even more power is needed while driving uphill. Slope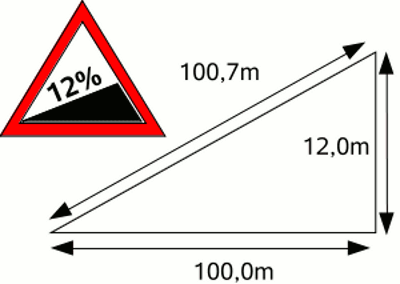
Looking at formula [2.11] shows that work is done when a body is lifted. Accordingly a car needs power to move uphill with constant speed. Grades at road traffic are given in percent. Slope is calculated as a ratio of "rise over run" in which run is the horizontal distance and rise is the vertical distance. A slope of 12% means the height difference is 12 meters while driving 100 meters. Note that the really driven distance to climb 12 meters is slightly longer (in this case 100,7m). Contrary the climbed height difference per 100m driving distance can be calculated as followed: Δhis = 100 * Δhgiv / √(1002 + Δhgiv2) Where is: Δhis - height difference per 100m driving distance, Δhgiv - height difference per 100m horizontal distance It is:
EPot - potential energy, m - mass, g - gravitational acceleration, h - height difference, P - power, t - time, x - height difference per 100m driving distance given in Percent, s - distance, v - speed
A lot of power to climb up a hill. Unpayable is the fact that those power is handed back while driving downhill. Energy used to overpower air or rolling resistance is inevitably lost. Rolling resistance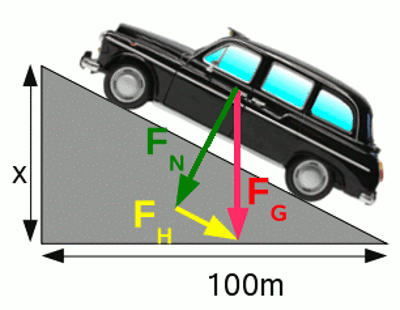
The lowest loss of power is caused by rolling resistance. As demonstrated by formula [2.5], the force trying to slow down a car is independent from the driving speed. Just the normal force being perpendicular to the street is part of the calculation. While driving horizontally, this force equals the gravitational force. While driving up- or downhill, the gravitational force is split into frictional force acting parallel to the street and the normal force acting perpendicular to the street. Slope and normal force are correlated as followed: FH / FN = x / 100 or FH = x * FN / 100 Using the Pythagorean theorem gives: FH2 + FN2 = FG2 or FN = √(FG2 / (x2 / 10000 + 1)) The rolling resistance coefficient of a car tire with the correct air pressure is about 0,012. While driving horizontally on a street meaning with the maximal normal force, we get: FR = 0,012 * 765kg * 9,81m/s2 = 90,0558N (FR is reduced to 89.0595N at a 15% slope) The loss of power is: ER = FR * s = P * t or P = FR * s / t = FR * v Where is: FR - Force caused by rolling friction, s - distance, t - time, v - speed, ER - loss of energy caused by rolling friction, P - power
News The Project Technology RoboSpatium Contribute Subject index Archives Download Responses Games Links Gadgets Contact Imprint |
|
|