|
|
|
|
News The Project Technology RoboSpatium Contribute Subject index Download Responses Games Gadgets Contact <<< Magnetism Magnetic permeability >>> InductorMagnetic field of a point charge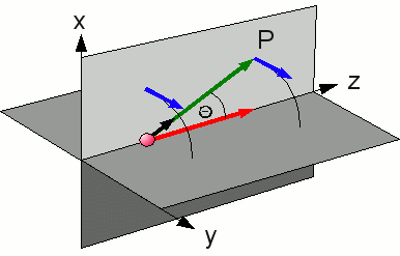
The field lines of a point charge, moving with constant velocity, are running in circles around the axis of movement. At this picture the positive charged particle is moving to the right along the z-axis. When looking at the direction of movement, the field lines are running clockwise. The dark blue arrows symbolize the magnetic flux density and the red arrow the velocity of the particle. For the magnetic flux density at the distance r from the particle there is: Where is: B - Magnetic flux density, μ - magnetic permeability, q - charge, v - velocity, r - distance, n - unit vector pointing from the particle to point P For the absolute value of the magnetic flux density we get: Where is: B - Magnetic flux density, μ - magnetic permeability, q - charge, v - velocity, r - distance, Θ - angle between v and r Magnetic field of a straight wireAs mentioned before, the electric current of a wire is caused by moving electrons. The magnetic field of the wire is the superposition of the fields of the single electrons. The magnetic flux density of a straight wire with an infinite length is given by:Where is: B - Magnetic flux density, μ - magnetic permeability, I - current, r - distance This formula can also be applied when a wire with a finite length is observed, as long as the value of r is small in comparison to the length of the wire. Near the endings of the wire and at great distances, the shape of the magnetic field is different from those of a wire with infinite length. Superposition of magnetic fieldsAs seen at the previous page, magnetic fields can superpose, resulting in higher or lower strength of the resulting field (at least at some areas). To increase the strength of the magnetic field, caused by a wire, you have to put one ore more wires in parallel to the first one. The electric current has to pass the parallel wires in the same direction. The most simple way to arrange wires side by side is to wind one long wire on a pipe or rod. This results in many close by windings, an electric current passes in the same direction. This arrangement increases the strength of the resulting magnetic field (locally).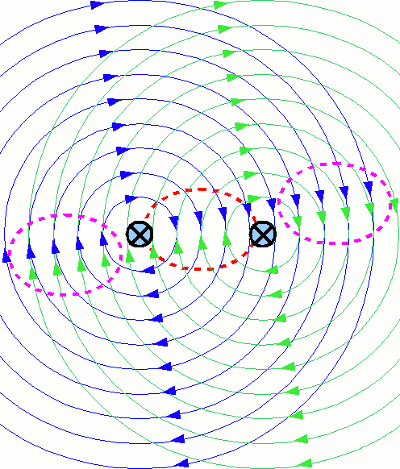
Magnetic field lines of two wires passed by an electric current: This picture shows the cross section of two wires side by side. The current is pointing towards the screen, illustrated by the crosses, who symbolize arrows seen from behind. The resulting magnetic field lines are concentric circles running clockwise with the wires at their center. The field lines of the left wire are painted blue, those of the right wire are painted green. The field lines run in circles as long as a current passes just one of the wires. If the electric current passes both wires, the magnetic fields superpose each other. As you can see at the picture the (non superposing) field lines are running contrary at the red marked area and in the same direction at the pink marked areas. Therewith the magnetic field is weakened at the red marked area and enforced at the pink marked areas. 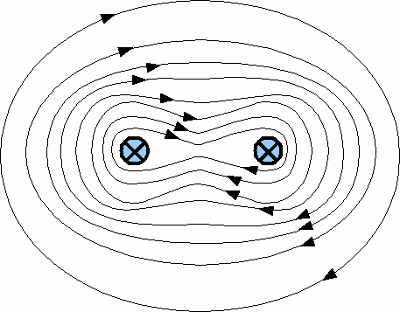
This drawing shows the resulting magnetic field of two parallel arranged wires with an electric current running into the screen. The field lines are pushed aside at the space between the wires and they become oval and finally circular at the space around the two wires. Looking at the two wires from a great distance, it looks like being the magnetic field of a single wire with the double current passing through. The magnetic field is weakened between the wires and enforced around them. The resulting force is attracting the two wires. 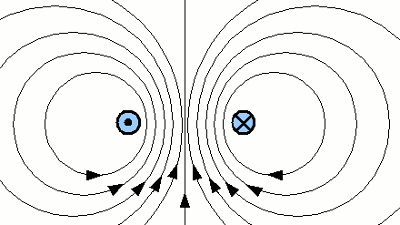
If the current is passing the wires in opposite direction (left wire coming from the screen, right wire pointing towards the screen), the magnetic field is enforced at the space between the wires and weakened around the two wires. The result is a force repelling the two wires. 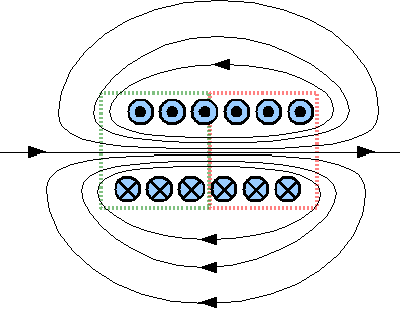
This drawing shows the cross section of a coil with 6 windings, The current is pointing towards the screen at the lower half (cross, symbolizing the back of an arrow) and pointing out of the screen at the upper half of the coil (point, symbolizing the tip of an arrow). The resulting field lines are running clockwise at the lower half and anticlockwise at the upper half. Furthermore the field lines are exiting the coil at the right side and entering at the left side. The magnetic field is similar to those of a bar shaped permanent magnet with the south pole at the left (green rectangle) and the north pole at the right of the coil (red rectangle). As mentioned above, forces are acting between current-carrying wires. Therefore the coil is compressed between the left and right side and a "positive pressure" is acting from the center in radial direction to the outside of the coil. Those forces should not be neglected at inductors carrying high currents hence with a high magnetic field strength (particle accelerators)! The magnetic field of an inductor is enforced at the inside by the superposition of the magnetic field lines of the wire windings. The field lines are almost parallel at the inside of the inductor, meaning the magnetic field is homogeneous at this area. The magnetic flux density at the center of an inductor with n windings, whose length is large in comparison to it's diameter, can be calculated as followed: Where is: B - Magnetic flux density, μ - magnetic permeability, I - current, n - number of windings, l - length of the inductor Biot-Savart lawIn general, the magnetic field generated by a steady current can be computed by using the Biot-Savart law:Where is: B - Magnetic flux density, dV - differential element of volume, J - current density in the volume dV, μ0 - magnetic permeability, r - vector from dV to the point at which the field is being computed This law can be simplified when the current can be approximated as running through an infinitely-narrow wire: Where is: B - Magnetic flux density, dV - differential element of volume, I - current running through the wire, μ0 - magnetic permeability, r - vector from dV to the point at which the field is being computed 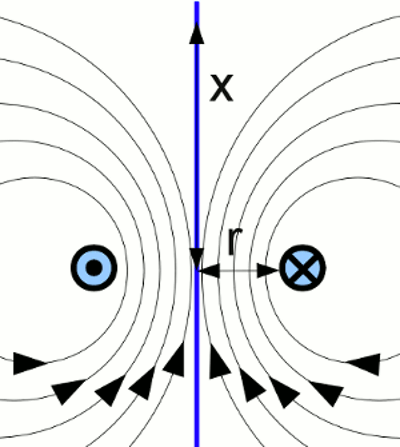
With the help of this law, we get for the flux density of one single conductor loop: Where is: B - Magnetic flux density, I - current running through the wire, μ0 - magnetic permeability, r - radius of conductor loop, x - distance from the center point of the conductor loop to the point at the middle axis The magnetic flux density of [3.20] and [3.21] (see above) can be derived with the help of the Biot-Savart law, too. <<< Magnetism Magnetic permeability >>> News The Project Technology RoboSpatium Contribute Subject index Archives Download Responses Games Links Gadgets Contact Imprint |
|
|